
Many of the Pragyan crypto challenges could be summed up as find a ciphertext, then find a relevant cipher and solve it. I’ve got one of those solutions and one other solution for this writeup.
In the former category we have Kill the devil. A 60 point challenge featuring a downloadable file “Problem.txt”. We grab the file and check it out:
root@kali:~/pragyan/crypto/kill-the-devil# file Problem.txt
Problem.txt: ASCII text
root@kali:~/pragyan/crypto/kill-the-devil# cat Problem.txt
4c6544144496414154444f434550474e5464857595241
Prior to the hint (shown above) being posted we tried a few methods to decode this, suspecting it to be a hex encoded ASCII string but the string contains an odd number of characters and if we zero pad it it does not decode to printable characters.
We found that “Kill the Devil” referred to killing or deleting the numbers 666. There are 3 “6” characters exactly in the Problem.txt. We remove and now can decode successfully!
root@kali:~/pragyan/crypto/kill-the-devil# python -c 'print open("Problem.txt","r").read().strip().replace("6","").decode("hex")'
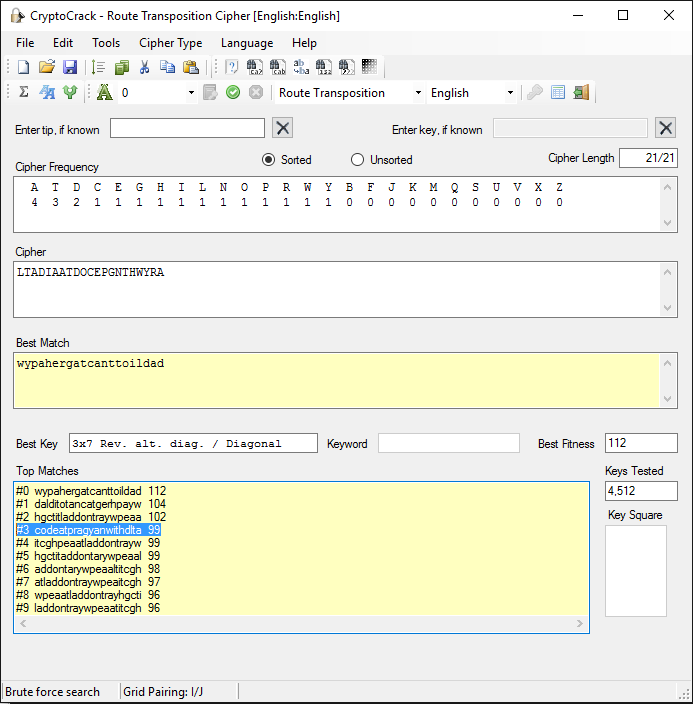
LTADIAATDOCEPGNTHWYRA
Great ! But a ciphertext it seems. We analyse it with Crypto Crack and find the top 5 probable ciphers as follows:
IC: 48, Max IC: 142, Max Kappa: 333
Digraphic IC: 0, Even Digraphic IC: 0
3-char repeats: 0, Odd spaced repeats: 50
Avg digraph: 610, Avg digraph discrep.: 129
Most likely cipher type has the lowest score.
Running Key............24
Double CheckerBoard....27
Route Transp...........31
Seriated Playfair......32
Nihilist Transp........32
We rule out CheckerBoard ciphers since it needs an even number of ciphertext characters. We try many variations of Running Key attacks, brute force and dictionary attacks with no luck. Finally we try Route Transposition and get lucky and spot the flag:
RSA_Encryption
For this one I just happened to be up late at night when they posted this one. I noticed about an hour after it was posted and solved it easily. It’s called RSA_Encryption and comes with a file called “rsaq”.
This file is a TGZ file which we extract to three files. key1_data.txt, key2_data.txt and ciphertext.txt. The key files contain a value of n and e, for example:
Public key :
n1 =
123948613128507245097711825164030080528129311429181946930789480629270692835124562568997437300916285601268900901495788327838386854611883075845387070635813324417496512348003686061832004434518190158084956517800098929984855603216625922341285873495112316366384741709770903928077127611563285935366595098601100940173
e = 65537
These are RSA public keys as the title of the challenge suggests. The ciphertext.txt is just a base64 encoded binary file.
The first thing I notice is that the keys are large but there’s two of them. Why two keys?
Something about large integers which makes RSA secure is that factoring large integers is really hard. However if you have two large integers, finding a common divisor is actually simple and quick using the Euclidean algorithm. If you can find a common divisor between two RSA modulii then you’ve found one of it’s factors!
I used the libnum gcd() function but you can use the standard libary GCD function (from fractions import gcd) or write your own in a few lines of code. This produced a result immediately so I was happy.
root@kali:~/pragyan/crypto/rsa# python
Python 2.7.11 (default, Jan 11 2016, 21:04:40)
[GCC 5.3.1 20160101] on linux2
Type "help", "copyright", "credits" or "license" for more information.
>>> import libnum
>>> n1 = 123948613128507245097711825164030080528129311429181946930789480629270692835124562568997437300916285601268900901495788327838386854611883075845387070635813324417496512348003686061832004434518190158084956517800098929984855603216625922341285873495112316366384741709770903928077127611563285935366595098601100940173
>>> n2 = 122890614849300155056519159433849880305439158904289542874766496514523043027349829509818565800562562195671251134947871996792136355514373160369135263766229423623131725044925870918859304353484491601318921285331340604341809979578202817714205469839224620893418109679223753141128229197377934231853172927071087589849
>>> libnum.gcd(n1,n2)
10217448931214694338056485232749303426398394639721270661250957562469575452791285994591928128667427053613383890906224746410843946303710562036668193362502553L
Now that we’ve found one factor, we can simply calculate the other factor, find ![]() {.image} and then solve for _d _using modular inversion which is handily built into the libum library!
{.image} and then solve for _d _using modular inversion which is handily built into the libum library!
Here’s my solution in Python:
#!/usr/bin/python
import base64
import libnum
n1 = 123948613128507245097711825164030080528129311429181946930789480629270692835124562568997437300916285601268900901495788327838386854611883075845387070635813324417496512348003686061832004434518190158084956517800098929984855603216625922341285873495112316366384741709770903928077127611563285935366595098601100940173
n2 = 122890614849300155056519159433849880305439158904289542874766496514523043027349829509818565800562562195671251134947871996792136355514373160369135263766229423623131725044925870918859304353484491601318921285331340604341809979578202817714205469839224620893418109679223753141128229197377934231853172927071087589849
e = 65537
q = libnum.gcd(n1,n2) # calculate gcd to discover a prime factor in common
p = n1 / q
phi = (p-1) * (q - 1)
c = libnum.s2n(base64.b64decode(open('ciphertext.txt','r').read()))
d = libnum.invmod(e,phi)
m = pow(c,d,n1)
print "[+] Flag: " + libnum.n2s(m)
Which produce the flag:
root@kali:~/pragyan/crypto/rsa# ./solve.py
[+] Flag: Congrats! The flag is nothing_is_impossible