BKP for 2016 is over, fantastic CTF and this year they stepped it up with the difficulty and quality of challenges. BKP last year was the first CTF I’ve ever done so revisting BKP felt very sentimental for me.
I liked the look of this challenge when it was posted during the CTF because I love me some RSA attacks. The clue read:
Alice and bob are close together, likely because they have a lot of things in common. This is why Alice asked him a small *q*uestion, about something cooler than a wiener.
This set all my alarms ringing. Are they describing the attack to use here? Who knows? Let’s dive in!
The challenge file we receive is a simple ZIP file with three files within:
-rw-rw-r-- 1 root root 128 Mar 5 19:37 almost_almost_almost_almost_there.encrypted
-rw-rw-r-- 1 root root 271 Mar 5 19:37 almost_almost_almost_almost_there.pub
-rw-rw-r-- 1 root root 2342 Mar 5 19:37 almost_almost_almost_almost_there.zip
A public key, a ciphertext binary file and another ZIP? The second ZIP file is password protected but we can still see the filenames that it contains within by giving an invalid password to unzip:
root@kali:~/bkp/crypto/bob# unzip -P wrong almost_almost_almost_almost_there.zip
Archive: almost_almost_almost_almost_there.zip
skipping: almost_almost_almost_there.encrypted incorrect password
skipping: almost_almost_almost_there.pub incorrect password
skipping: almost_almost_almost_there.zip incorrect password
Another public key, ciphertext and zip file? Using these clues, plus the filename clues, it appears we have one of those “Layer” challenges. Typically we see these with recursive or obscure compression algorithms but not seen this with RSA before.
The first thing I do is extract the public key from the .pub file using OpenSSL command line tool to check the size and look for any obvious inconsistencies:
root@kali:~/bkp/crypto/bob# openssl asn1parse -in almost_almost_almost_almost_there.pub -strparse 18 0:d=0 hl=3 l= 137 cons: SEQUENCE
3:d=1 hl=3 l= 129 prim: INTEGER :86E996013E77C41699000E0941D480C046B2F71A4F95B350AC1A4D426372923D8A4561D96FBFB0240595907201AD3225CF6EDED7DE02D91C386FFAC280B72D0F95CAE71F42EBE0D3EDAEACE7CEA3195FA32C1C6080D90EF853D06DD4572C92B9F8310BBC0C635A5E26952511751030A6590816554E763031BCBB31E3F119C65F
135:d=1 hl=2 l= 3 prim: INTEGER :010001
root@kali:~/bkp/crypto/bob# python -c 'print int("86E996013E77C41699000E0941D480C046B2F71A4F95B350AC1A4D426372923D8A4561D96FBFB0240595907201AD3225CF6EDED7DE02D91C386FFAC280B72D0F95CAE71F42EBE0D3EDAEACE7CEA3195FA32C1C6080D90EF853D06DD4572C92B9F8310BBC0C635A5E26952511751030A6590816554E763031BCBB31E3F119C65F",16).bit_length()'
1024
1024 bit key and normal looking exponent (65537). Checking “factordb.com” shows the number is composite with no known factors. Ok. A re-read of the clue and our extended knowledge of the challenge so far gives us a hint:
- The filename is “almost_almost_almost_almost_there.*”, consisting of 4 x “almost”
- There are four sub-parts in the clue:
- Alice and bob are close together
- likely because they have a lot of things in common
- This is why Alice asked him a small *q*uestion
- about something cooler than a wiener.
Maybe each sub-part of the clue describes a layer? Let’s go with that!
Layer 1
Based on the assumption that each sub clue is a layer, this means layer one is “Alice and bob are close together”? That could mean that the prime numbers in this modulus are too close together? So this means the primes p and q for this modulus n may be similar to √n.
Using this idea I ask this online factorization tool knowing that if this is accurate it will recover the primes in no time. Within 12 seconds we have factored a 1024 bit modulus. Nice:
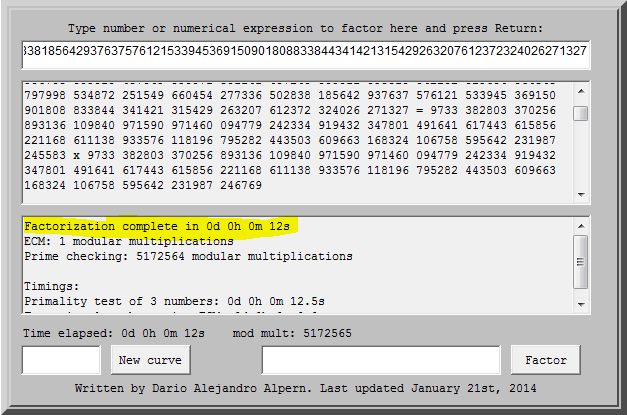
We take the p and q, compute d and recover the plaintext which predictably turns out to be the password to the next layer ZIP file. So we unzip the next public key, ciphertext, and ZIP file layer and settle in for a long challenge.
Layer 2
The next layer in our clue should be “likely because they have a lot of things in common”. Fine, “common” can describe a couple of things in RSA, common modulus and common factors being the top two off the top of my head! We examine the modulus:
root@kali:~/bkp/crypto/bob# openssl rsa -in almost_almost_almost_almost_there.pub -pubin -noout -modulus
Modulus=86E996013E77C41699000E0941D480C046B2F71A4F95B350AC1A4D426372923D8A4561D96FBFB0240595907201AD3225CF6EDED7DE02D91C386FFAC280B72D0F95CAE71F42EBE0D3EDAEACE7CEA3195FA32C1C6080D90EF853D06DD4572C92B9F8310BBC0C635A5E26952511751030A6590816554E763031BCBB31E3F119C65F
root@kali:~/bkp/crypto/bob# openssl rsa -in almost_almost_almost_there.pub -pubin -noout -modulus
Modulus=ABE633CEC2E7EC10A851927905A657DF4E10416023C0C34FC64D64BD8B8257B7BF207ADD047B0ADF21C525B052068C70295C746C3B1BE1436F39ED8BF7A813E4B845CE0CA89CA828B45763D46B1898C7A2FA5F8FE78428CAB6CDF70EF871DB971B3232841A1CE2459CE650A154362F80CFB64163C3CA63AD72BCFBDBF0154FF7
root@kali:~/bkp/crypto/bob#
Well it’s not a common modulus attack because the modulus differs from layer 1. We can check for common factors using the Euclidean algorithm to find the greatest common divisor (gcd). This is a very fast way to find one of the primes if the modulii share a factor:
root@kali:~/bkp/crypto/bob# python
Python 2.7.11 (default, Jan 11 2016, 21:04:40)
[GCC 5.3.1 20160101] on linux2
Type "help", "copyright", "credits" or "license" for more information.
>>> import fractions
>>> n1 = 0x86E996013E77C41699000E0941D480C046B2F71A4F95B350AC1A4D426372923D8A4561D96FBFB0240595907201AD3225CF6EDED7DE02D91C386FFAC280B72D0F95CAE71F42EBE0D3EDAEACE7CEA3195FA32C1C6080D90EF853D06DD4572C92B9F8310BBC0C635A5E26952511751030A6590816554E763031BCBB31E3F119C65F
>>> n2 = 0xABE633CEC2E7EC10A851927905A657DF4E10416023C0C34FC64D64BD8B8257B7BF207ADD047B0ADF21C525B052068C70295C746C3B1BE1436F39ED8BF7A813E4B845CE0CA89CA828B45763D46B1898C7A2FA5F8FE78428CAB6CDF70EF871DB971B3232841A1CE2459CE650A154362F80CFB64163C3CA63AD72BCFBDBF0154FF7
>>> fractions.gcd(n1,n2)
9733382803370256893136109840971590971460094779242334919432347801491641617443615856221168611138933576118196795282443503609663168324106758595642231987246769L
Woot! We have our factor and simply need to divide n / p to find q. We do that, derive d and recover this layer’s ciphertext.
Layer 3
Layer 3’s clue is “This is why Alice asked him a small *q*uestion”. Since “q” is bolded we assume it means that we’re looking at a modulus where one of the primes is small. Firstly we load the public key, gather the modulus and exponent and then run a standard factorization method using primes from 1 - 100,000. This is very quick:
root@kali:~/bkp/crypto/bob# openssl rsa -in almost_almost_there.pub -pubin -noout -modulus
Modulus=BAD20CF97ED5042DF696CE4DF3E5A678CF4FB3693D3DF12DFE9FD3FD8CC8AAB8B95533E414E3FC0C377F4EE54827118B1D30561A3C741BEA7C76899789B51743E076092DF9EB05DC97EB1505CE9EB12B5AB9E10ABF56F920A58E7E00ECF05977E872834DD8584CF4AC87CB7DC50159BD962C75CBEFB6C6AC3A31A74E7D8F1E4C10D5
root@kali:~/bkp/crypto/bob# python
Python 2.7.11 (default, Jan 11 2016, 21:04:40)
[GCC 5.3.1 20160101] on linux2
Type "help", "copyright", "credits" or "license" for more information.
>>> import libnum
>>> n3 = 0xBAD20CF97ED5042DF696CE4DF3E5A678CF4FB3693D3DF12DFE9FD3FD8CC8AAB8B95533E414E3FC0C377F4EE54827118B1D30561A3C741BEA7C76899789B51743E076092DF9EB05DC97EB1505CE9EB12B5AB9E10ABF56F920A58E7E00ECF05977E872834DD8584CF4AC87CB7DC50159BD962C75CBEFB6C6AC3A31A74E7D8F1E4C10D5
>>> for prime in libnum.primes(100000):
... if n3 % prime == :
... print "q = " + str(prime)
...
q = 54311
>>>
Yay, super fast! We have q, one of the primes that make up our modulus. We divide n/q to recover p, then derive d and solve for m!
Next round please!
Layer 4
This is the fourth and final layer of this challenge. This one’s clue is direct as well “about something cooler than a wiener”. Yawn! Wiener attack in a CTF again!? Nah just kidding please keep doing this as I enjoy points.
Wiener attack is easy to spot in general because exponents tend to be huge. Instead of the recognized “normal” value of e = 0x10001 (65537) keys succepitble to Wiener’s attack typically see exponents closer to the modulus in size. Here’s what layer 4’s values of n and e looked like:
root@kali:~/bkp/crypto/bob# openssl asn1parse -in almost_there.pub -strparse 19
0:d=0 hl=4 l= 263 cons: SEQUENCE
4:d=1 hl=3 l= 129 prim: INTEGER :9C2F6505899120906E5AFBD755C92FEC429FBA194466F06AAE484FA33CABA720205E94CE9BF5AA527224916D1852AE07915FBC6A3A52045857E0A1224C72A360C01C0CEF388F1693A746D5AFBF318C0ABF027661ACAB54E0290DFA21C3616A498210E2578121D7C23877429331D428D756B957EB41ECAB1EAAD87018C6EA3445
136:d=1 hl=3 l= 128 prim: INTEGER :466A169E8C14AC89F39B5B0357EFFC3E2139F9B19E28C1E299F18B54952A07A932BA5CA9F4B93B3EAA5A12C4856981EE1A31A5B47A0068FF081FA3C8C2C546FEAA3619FD6EC7DD71C9A2E75F1301EC935F7A5B744A73DF34D21C47592E149074A3CCEF749ECE475E3B6B0C8EECAC7C55290FF148E9A29DB8480CFE2A57801275
In this output, the modulus (n) is the first long integer and the public exponent (e) is the second long integer.
We use code from past CTF challenges to solve for d given n and e and decrypt the ciphertext.
This time it gives us the password to the ZIP file containing 1 single file, “FLAG”. Joy of joys it’s over!
root@kali:~/bkp/crypto/bob# cat FLAG
BKPCTF{Its_not_you,_its_rsa_(that_is_broken)}
Full solution source code here for laughs! Download it and associated files on Github.
#!/usr/bin/python
import libnum
import subprocess
################### LAYER 1 ######################
print "[*] Solving layer 1: Weak key factored with ECM method"
# layer 1 public key
n = 94738740796943840961823530695778701408987757287583492665919730017973847138345511139064596113422435977583856843887008168202003855906708039013487349390571801141407245039011598810542232029634564848797998534872251549660454277336502838185642937637576121533945369150901808833844341421315429263207612372324026271327
e = 65537
# layer 1 factored with ECC method
p = 9733382803370256893136109840971590971460094779242334919432347801491641617443615856221168611138933576118196795282443503609663168324106758595642231987245583
q = 9733382803370256893136109840971590971460094779242334919432347801491641617443615856221168611138933576118196795282443503609663168324106758595642231987246769
# valid p and q right!?
assert(n % p == )
assert(n % q == )
c = libnum.s2n(open('almost_almost_almost_almost_there.encrypted','rb').read())
phi = (p - 1) * (q - 1)
d = libnum.invmod(e, phi)
m = pow(c,d,n)
zippassword = libnum.n2s(m)
################### LAYER 2 ######################
print "[*] Solving layer 2: Common factors!"
# unzip layer2
unzip = subprocess.check_output(['unzip','-o','-P',zippassword,'almost_almost_almost_almost_there.zip'])
# get next modulus
l2n = int(subprocess.check_output(['openssl', 'rsa', '-noout', '-modulus', '-pubin', '-in', 'almost_almost_almost_there.pub']).split('=')[1],16)
# load ciphertext
l2c = libnum.s2n(open('almost_almost_almost_there.encrypted','rb').read())
# layer 2 modulus has common factor with layer 1
l2q = libnum.gcd(l2n, n)
l2p = l2n / l2q
l2phi = (l2p - 1 ) * (l2q - 1)
l2d = libnum.invmod(e, l2phi)
l2m = pow(l2c, l2d, l2n)
l2zippass = libnum.n2s(l2m)
################### LAYER 3 ######################
print "[*] Solving layer 3: Small q "
unzip = subprocess.check_output(['unzip','-o','-P',l2zippass,'almost_almost_almost_there.zip'])
l3n = int(subprocess.check_output(['openssl', 'rsa', '-noout', '-modulus', '-pubin', '-in', 'almost_almost_there.pub']).split('=')[1],16)
l3c = libnum.s2n(open('almost_almost_there.encrypted','rb').read())
# small q, factored using ECM method or any simple method
l3q = 54311
l3p = l3n / l3q
l3phi = (l3p - 1) * (l3q - 1)
l3d = libnum.invmod(e, l3phi)
l3m = pow(l3c,l3d,l3n)
l3zippass = libnum.n2s(l3m)
################### LAYER 4 ######################
print "[*] Solving layer 4: Wieners attack!"
unzip = subprocess.check_output(['unzip','-o','-P',l3zippass,'almost_almost_there.zip'])
l4key = [(int(x.split(':')[3],16)) for x in subprocess.check_output(['openssl', 'asn1parse', '-in', 'almost_there.pub','-strparse','19']).splitlines() if 'INTEGER' in x]
l4c = libnum.s2n(open('almost_there.encrypted','rb').read())
# use Wiener attack to find d from n and e
from wiener import wiener
l4d = wiener(l4key[1],l4key[])
l4m = pow(l4c, l4d, l4key[])
l4zippass = libnum.n2s(l4m)
############## GET FLAG ###############
unzip = subprocess.check_output(['unzip','-o','-P',l4zippass,'almost_there.zip'])
print "[+] Flag: " + open('FLAG','r').read()